Equivalencia de infinitésimos

Una Exploración Profunda

En el vasto mundo de las matemáticas, hay conceptos que desafían nuestra intuición y nos llevan a explorar los límites de nuestro entendimiento. Uno de estos conceptos intrigantes es el de los infinitésimos. Aunque pueden parecer abstractos e incluso misteriosos al principio, los infinitésimos juegan un papel fundamental en el cálculo y en nuestra comprensión del cambio continuo. En este artículo, exploraremos qué son los infinitésimos, cómo se relacionan con conceptos más familiares y cómo se utilizan en diversas áreas de las matemáticas y la física.

El Significado de Infinitésimo

Para comprender los infinitésimos, primero debemos entender el concepto de infinito. En matemáticas, el infinito representa una cantidad que no tiene límite superior o inferior. Por otro lado, un infinitésimo es una cantidad extremadamente pequeña, tan pequeña que, en términos precisos, es menor que cualquier número real positivo, pero aún mayor que cero.

Este concepto puede parecer paradójico o incluso contradictorio, ya que la idea de algo “tan pequeño que es casi nada pero aún no es nada” desafía nuestra intuición. Sin embargo, en el marco del cálculo y el análisis matemático, los infinitésimos tienen un significado preciso y se utilizan para describir el cambio instantáneo en una función o la pendiente de una curva en un punto específico.

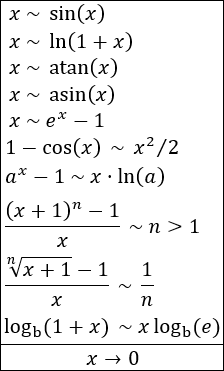
Infinitésimos y Derivadas

Una de las aplicaciones más importantes de los infinitésimos es en el cálculo de derivadas. La derivada de una función en un punto dado representa la pendiente de la curva en ese punto. En términos más simples, indica cómo cambia la función cuando el valor de la variable independiente cambia muy poco alrededor de ese punto.

Los infinitésimos nos permiten expresar esta idea de cambio instantáneo de manera precisa. Por ejemplo, si tenemos una función $f(x)$, la derivada de $f(x)$ en un punto $x$ se puede definir como:

f′(x)=lim h→0​ (f(x+h)−f(x)) /h​

Aquí, el término ℎ representa un infinitésimo, ya que se acerca infinitamente a cero pero no es exactamente cero. Esta expresión nos dice cómo cambia el valor de $f(x)$ cuando $x$ cambia en una cantidad infinitesimal alrededor del punto $x$.

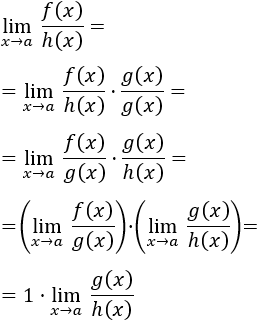
La Regla de L’Hôpital

Otro ejemplo destacado del uso de infinitésimos es la regla de L’Hôpital, que proporciona un método para evaluar límites indeterminados de funciones. La regla establece que, bajo ciertas condiciones, el límite de la razón de dos funciones es igual al límite de las derivadas de esas funciones.

Esta regla es invaluable en el cálculo de límites que de otra manera serían difíciles de resolver.

Aplicaciones en la Física y otras Ciencias

Los infinitésimos no solo son importantes en matemáticas puras, sino que también tienen aplicaciones significativas en la física y otras ciencias. Por ejemplo, en la física, los infinitésimos se utilizan para describir el movimiento de objetos en el espacio y el tiempo. Las derivadas e integrales, que dependen de los infinitésimos, son fundamentales para formular leyes físicas y resolver problemas en áreas como la mecánica, la termodinámica y la electromagnetismo.

Críticas y Controversias

A pesar de su utilidad, el concepto de infinitésimo no ha estado exento de críticas y controversias a lo largo de la historia de las matemáticas. En particular, hubo un debate significativo en torno a la rigurosidad de los infinitésimos en los siglos XVII y XVIII, cuando algunos matemáticos cuestionaron su validez lógica.

Sin embargo, con el desarrollo del cálculo diferencial e integral por parte de matemáticos como Newton y Leibniz, los infinitésimos encontraron una base sólida y fueron aceptados como herramientas legítimas para el análisis matemático.

Conclusión